Druhy čísel

V průběhu matematické historie bylo objeveno několik číselných oborů - od kladných celých čísel až po čísla komplexní. Ty nejjednoduší, kterými udáváme počet, jsou kladná celá čísla a označujeme je přívlastkem přirozená (značíme N z anglického naturals). Spolu se zápornými čísly a nulou tvoří přirozená čísla množinu čísel celých (Z - z německého Zahlen).

Do množiny racionálních čísel, která se značí Q (z latinského quotient), patří celá a lomená čísla. Racionální čísla vyjadřujeme jako zlomek dvou celých čísel: a/b, kde b je různé od nuly. Další z druhů čísel je množina iracionálních čísel. Iracionální čísla nelze zapsat jako podíl dvou čísel, mají nekonečný desetinný rozvoj. Sem patří například pí = 3,141592654... (Ludolfovo číslo), e = 2,718281828... (Eulerovo číslo) nebo odmocnina ze 2 = 1,414213562...

Racionální a iracionální čísla tvoří množinu reálných čísel (R). Když si představíme nekonečnou přímku, pak reálná čísla představují všechny body na této přímce. Ale ani reálnými čísly náš výčet množin nekončí. Ještě zde máme čísla komplexní (C), která sdružují reálná čísla s těmi imaginárními. Všechny číselné množiny shrnuje následující schéma.

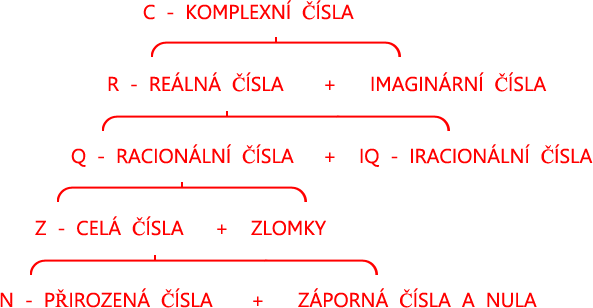
Zbývá vysvětlit, co znamenají imaginární a komplexní čísla. Komplexní číslo je číslo ve tvaru a+bi, kde a a b jsou reálná čísla a i značí imaginární jednotku. Ta je definována jako druhá odmocnina z mínus jedné. Vrátíme-li se ke geometrickému vyjádření, pak komplexní čísla leží v komplexní (Gaussově) rovině. Reálným číslům patří opět nekonečná přímka (osa x). Imaginární čísla potom leží na ose y, která je k ose x kolmá.

Komentáře k článku