Tempa růstu a pravidlo sedmdesáti

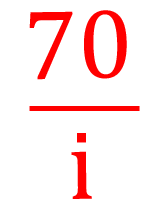V ekonomii a financích je dobré znát přibližnou odpověď na otázky tohoto typu: Pokud ekonomika nějaké země roste tempem 2 % ročně, za jak dlouho se její HDP zdvojnásobí? Nebo z jiného soudku: Když uložím do banky určitou částku na 2% roční úrok, za jak dlouho budu mít na účtu dvojnásobek? Těm, kterým je znám efekt složeného úročení, je jasné, že ta doba bude kratší než 50 let (a ti, kterým složené úročení nic moc neříká, se s ním mohou seznámit zde). Jak ale tento časový interval přesně či alespoň přibližně určit? Matematik by chvíli logaritmoval a pak by řekl, že výsledek se rovná cca 35,0028 let. Člověk znalý pravidla sedmdesáti by bez dlouhého přemýšlení prohlásil, že to bude trvat přibližně 35 let. Když provedeme kontrolu, zjistíme, že mají pravdu: (1+0,02)^35 = 1,999.. což je takřka hledaný dvojnásobek. Ukážeme si, jak na to přišli.

Použít pravidlo sedmdesáti je velice jednoduchý a rychlý způsob, jak tuto úloho vyřešit. Číslo 70 stačí vydělit tempem růstu v procentech a máme přibližný výsledek. V našem příkladě je to: 70/2 = 35 let (měli jsme roční tempo růstu, proto je také výsledek v letech). Asi se ptáte, proč zrovna 70? Vše se vysvětlí, až si tuto úlohu spočítáme obecně. Vyjdeme ze vzorce pro složené úročení, který obsahuje tři parametry: počáteční částku (P0), úrokovou sazbu (i) a počet období (n). Naším úkolem je vyřešit následující rovnici s neznámou n:

Je evidentní, že obě strany rovnice můžeme vydělit parametrem P0. Hledáme dvojnásobek nějaké částky, na jejíž velikosti vůbec nezáleží, proto ani v zadání příkladu nebyla definována. Rovnice přejde do tvaru:

Neznámá v exponentu nám řešení poměrně komplikuje. Bez trochy toho logaritmování se bohužel neobejdeme. Použijeme jednu ze základních vět o logaritmech (více o počítání s logaritmy zde). Abychom dostali neznámou z exponentu, musíme obě strany rovnice zlogaritmovat. Provedeme to přirozeným logaritmem (značí se ln) z důvodu, který se ozřejmí následně.

Zmíněná věta se dá zhruba formulovat jako: logaritmus mocniny se rovná násobku logaritmu. Zjednodušeně řečeno, tahle věta nám umožňuje vzít exponent a strčit ho před logaritmus:

Nyní už stačí jenom na levé straně rovnice osamostatnit n a pro hledanou neznámou dostaneme výsledek:

Na tomto místě bychom mohli skončit. S tímto vztahem a kalkulačkou snadno dojdeme k uvedenému výsledku našeho příkladu: ln 2/ln 1,02 = 35,0028.. Zbývá nám ovšem vysvětlit, kde se vzala ona tajemná sedmdesátka. Trochu nám napoví, když si najdeme hodnotu přirozeného logaritmu v bodě dva: ln 2 = 0,693.. Když toto číslo vynásobíme stem, dostaneme v čitateli necelých 70, což zatím není příliš přesvědčivé. Ještě ale musíme prozkoumat jmenovatel zlomku. Pro relativně malé hodnoty parametru i (ne více než 0,1) přibližně platí:

Když parametr i, který je ve formě desetinného čísla, vynásobíme stem, dostaneme ve jmenovateli tempo růstu v procentech. Těmito aproximacemi dostáváme pro pravidlo sedmdesáti výsledný tvar: n = 70 / x. Čitatel je zaokrouhlený nahoru na 70, protože také aproximované číslo ve jmenovateli je vždy o něco vyšší než by odpovídalo logaritmu (např. ln 1,02 = 0,00198.. tedy necelých 0,02). Když si funkci y = ln (1+x) zaneseme do grafu, ukáže se, proč byl zvolen právě přirozený logaritmus. Rovněž bude zřejmé, proč tato aproximace platí jen pro malé hodnoty čísla x.

Srovnání funkcí y = ln(1+x) a y = x

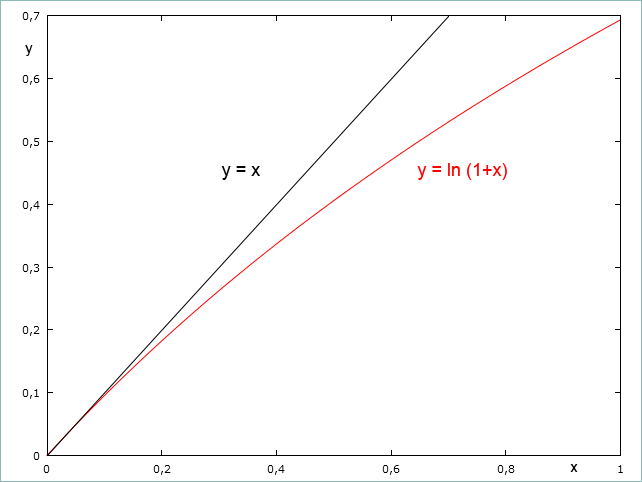
V intervalu 0 až 0,1 (0-10 %), kde jsou obě křivky funkcí v těsné blízkosti, je aproximace nejpřesnější. Jak se křivka logaritmu vzdaluje ose kvadrantu (přímce y=x), přesnost použití pravidla 70 znatelně klesá. Proto číslo 70 není jediné, které se v praxi používá. Často se můžeme setkat také s pravidlem 72, které je univerzálnější, protože je relativně přesné v intervalu 0 - 15 %. Na ještě vyšší tempa růstu je k lepší přesnosti možné použít pravidla s větším číslem (např. pravidlo 78 poskytuje dobré výsledky zhruba od 20 do 30 %).

My jsme si vše ukázali na pravidle 70, protože má dobré využití za současné ekonomické situace. Ekonomiky vyspělých zemí rostou jen o pár procent ročně. Také inflace a úrokové sazby se pohybují jen ve výši několika málo procent. Je třeba mít na paměti, že cílem tohoto pravidla je poskytnout rychlý orientační výpočet. Pravidlo 70 se dobře pamatuje, a pokud ho použijeme na relativně nízká tempa růstu, svému účelu poslouží více než dobře. Kdybychom měli pokaždé dlouze řešit, zda je vhodnější použít číslo 70, 72 či nějaké jiné, přínos této metody by citelně klesl. To už je rychlejší a lepší nic neaproximovat a zjistit si přesný výsledek za pomoci logaritmů.

Komentáře k článku